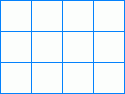
Figure 1: A 3x4 Grid
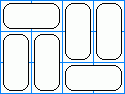
Figure 2: A domino tiling
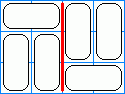
Figure 3: A cut in the tiling
Find rectangular grids G1 < G2 < G3 such that G1 and G3 admit uncuttable domino tilings, while G2 does not. Each has at least one side of even length and all grid sizes must be at least 2x2.(G1 is a subgrid of G2, which in turn is a subgrid of G3.)
A domino tiling of a rectangular grid is an arrangement of 2x1 tiles (dominoes) that covers all the grid squares. A tiling is cuttable if it can be split into two tilings of smaller rectangular grids by either a vertical or horizontal line. It is uncuttable otherwise.

Figure 1: A 3x4 Grid |

Figure 2: A domino tiling |

Figure 3: A cut in the tiling |
